阿里云开发者社区在线编程34.矩阵最小路径和

微wx笑 2020-07-16【算法】 6 0关键字：阿里云开发者社区在线编程矩阵最小路径

矩阵最小路径和概述：给定一个矩阵，大小为m，从左上角开始每次只能向右走或者向下走，最后达到右下角的位置。路径中所有数字累加起来就是路径和，返回所有路径的最小路径和。示例1比

矩阵最小路径和7O0无知

概述：7O0无知

给定一个矩阵，大小为m，从左上角开始每次只能向右走或者向下走，最后达到右下角的位置。路径中所有数字累加起来就是路径和，返回所有路径的最小路径和。7O0无知

7O0无知

示例1

比如输入矩阵为
4 1 5 3
3 2 7 7
6 5 2 8
8 9 4 5

最小路径为
23

解题思路：动态规划

此段内容引自：https://developer.aliyun.com/article/751327?spm=a2c6h.14164896.0.0.606270faPajFsS7O0无知

本题可以用动态规划的方法来解决。7O0无知

计算一个格子到右下角的最小路径需要两个数据，一个是右边格子到右下角的最小路径，一个是下边格子到右下角的最小路径，两个数据的较小值加上当前格子的数值即为最小路径。7O0无知

即 dp[i, j] = min(dp[i + 1, j], dp[i, j + 1]) + m[i, j]7O0无知

由于计算当前格子最小路径需要右边和下边格子的最小路径。因此，需要从底向上进行决策。7O0无知

本题用动态规划法的难点之一是从底向上进行决策的顺序。7O0无知

如下图所示，通过观察可以发现，同一对角线上的数字的横纵坐标和是相等的，我们以对角线的方向为顺序，从右下角向左上角计算出每个格子的最小路径。最后可计算得出 dp[0, 0]。7O0无知

7O0无知

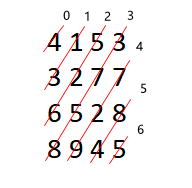
是不是有思路了呢，点击链接立刻答题：34.矩阵最小路径和7O0无知

正确解答

动态规划法

class Solution {
    public int solution(int[][] m) {
        return extracted(m);
    }

    private int extracted(int[][] arr) {
        int dp[][]=new int [arr.length][arr[0].length];
        dp[0][0]=arr[0][0];
        for(int i=1;i<arr.length;i++)
        {
            dp[i][0]=dp[i-1][0]+arr[i][0];
            //第一列只能由上向下
        }
        for(int j=1;j<arr[0].length;j++)
        {
            dp[0][j]=dp[0][j-1]+arr[0][j];
            //第一行只能由左向右
        }
        for(int i=1;i<arr.length;i++)
            for(int j=1;j<arr[0].length;j++)
            {
                dp[i][j]=Math.min(dp[i-1][j], dp[i][j-1])+arr[i][j];
            }

        return dp[arr.length-1][arr[0].length-1];
    }
}

嵌套循环法

相比上面的方法，此算法少了两次循环，但是算法有一个限制，必须是方阵。7O0无知

class Solution {
    public int solution(int[][] m) {
        int count = 0;
        for (int i=0;i<m.length -1;i++){
            for (int j=0;j<m[0].length -1;j++){
                if (i == j){
                    count += m[i][j];
                    if (m[i][j+1] <= m[i+1][j]){
                            count += m[i][j+1];
                        }else{
                            count += m[i+1][j];
                        }
                }
            }
        }
        count += m[m.length-1][m[0].length-1];
        return count;
    }
}